ENGINEERING MATHEMATICS
Geometry Coordinate, also known as Analytical Geometry, is a branch of mathematics that uses algebraic equations to describe and solve geometric problems on a Cartesian plane. This topic focuses on understanding how points, lines, and shapes can be represented and analyzed using coordinate systems.
Geometry Coordinate : Subtopics and Topics Learning Outcome

-
1.1 Cartesian Coordinate and Distance Formula
LO1: Explore the fundamentals of the Cartesian plane. Determine the distance and midpoint between two points. -
1.2 Equations of a Straight Line
LO2 : Construct equations of straight lines in various forms. -
1.3 Parallel and Perpendicular Lines
LO3 : Determine the properties of parallel and perpendicular lines. Find the equations of parallel and perpenducilar lines. -
1.4 Gradient and Angle Between Two Line
LO4 : Calculate the gradient of a straight line and determine the angle between twostraight lines..
How to use this module?
The lesson is divided into four stages. Starting from induction, Learning Activities, Learning Assesment, Conclusions and Reflections.

1 Inductions
This short introduction helps activate your prior knowledge. Begin by answering the quiz to assess your current understanding. Use all available resources to gather as much information as possible before diving into the lesson.
2 Learning Activities
Interactive tasks or exercises help students actively engage with and apply new knowledge or skills. In this activity, students are required to take notes from the narrated slides and videos, including all key points and examples.
3 Formative Assessment
Formative assessment involves ongoing checks (like quizzes, Q&A, or peer activities) to monitor student understanding and adjust teaching as needed. The assessment includes tutorial sheets and activities, which can be done individually or in pairs. Refer to the provided rubric as a guide for expectations.
4 Conclusions
Take time to reflect on what you’ve learned and wrap up the lesson. Identify the key parts you’ve understood, and refer to other sources for more details or deeper explanations.

OVERVIEW
✅ Learning Outcomes Summary:
By the end of this subtopic, students should be able to:
-
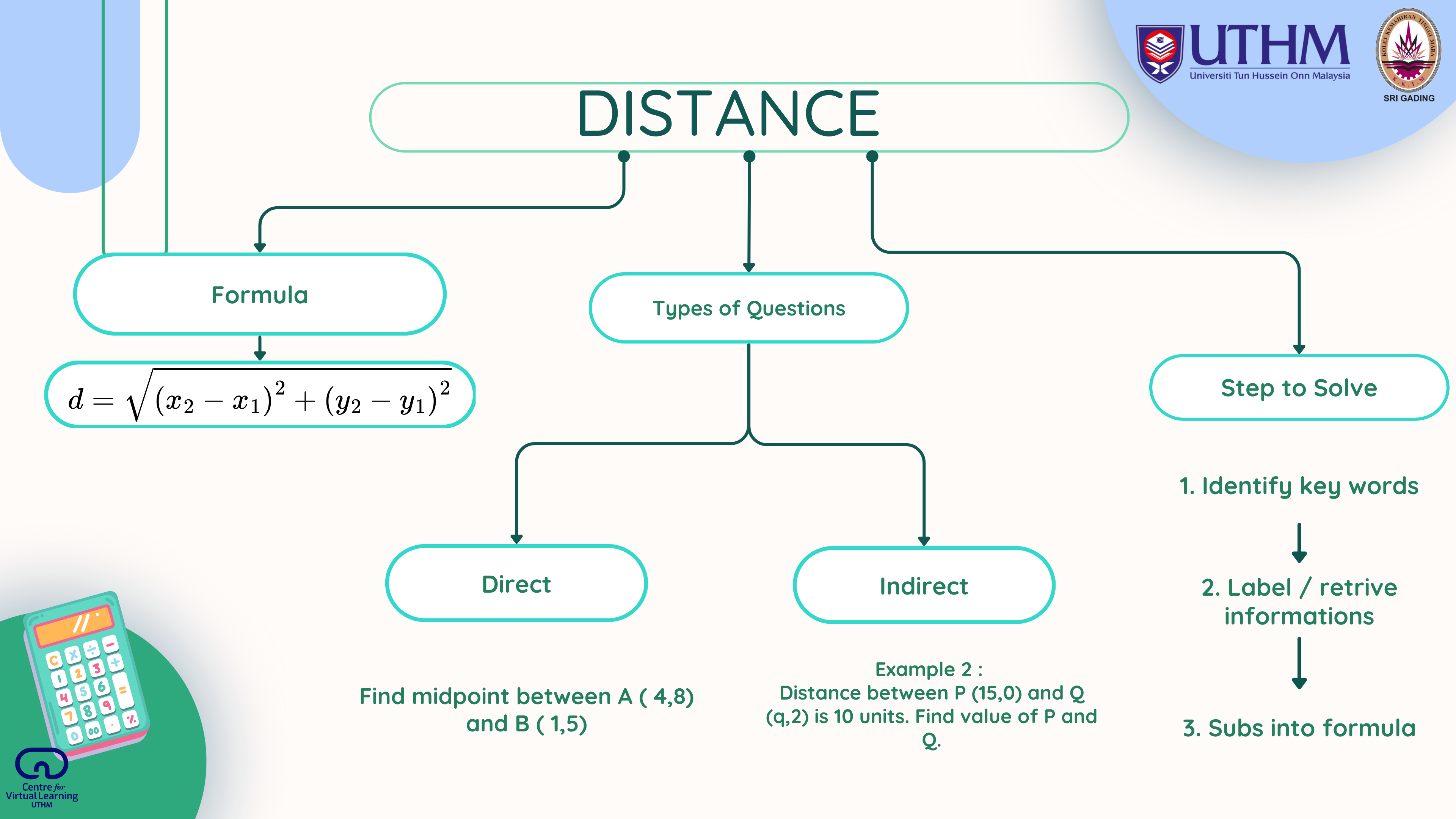
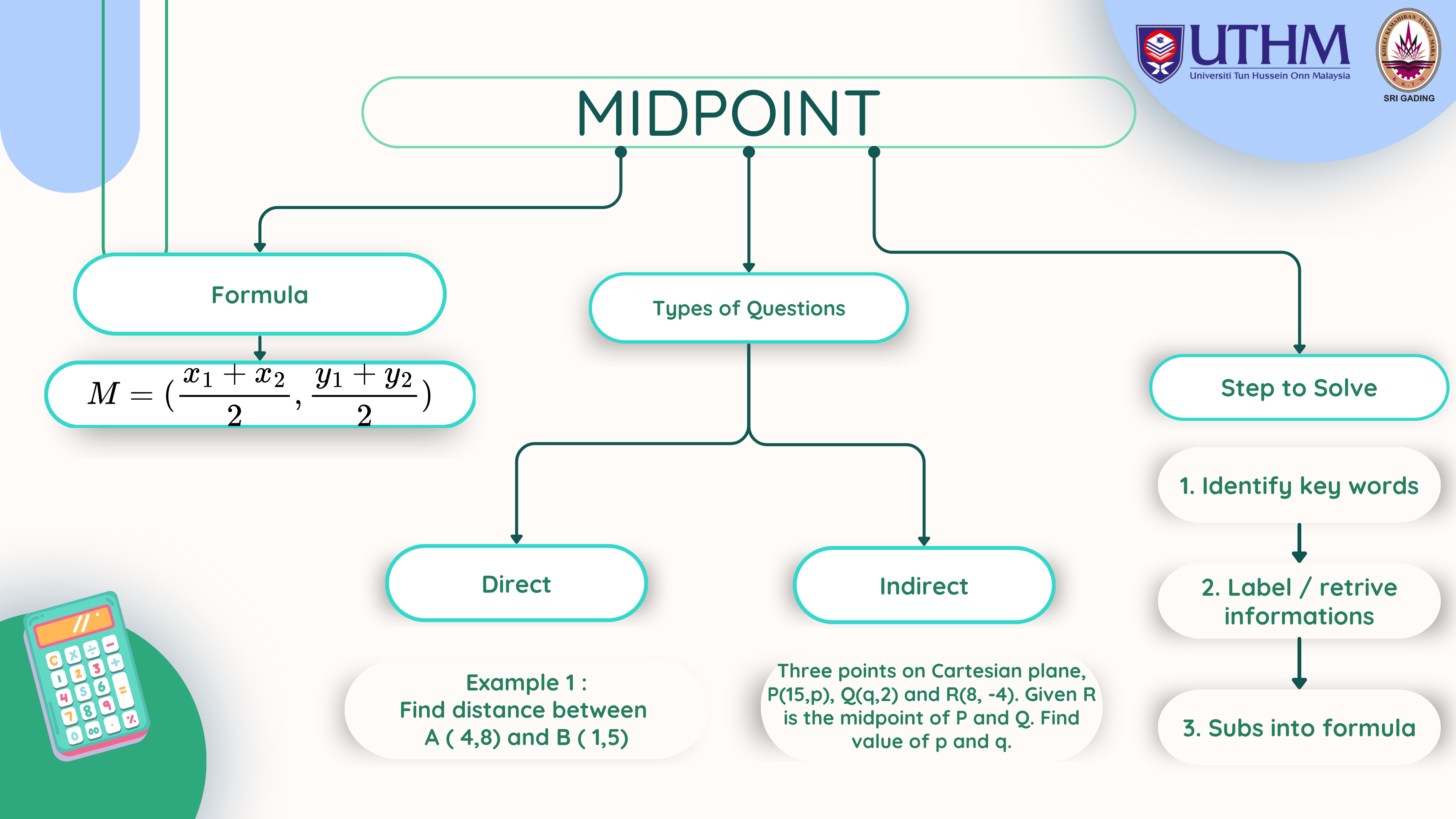
Calculate distance and midpoint between two points.
-
Determine unknowns using distance or midpoint formula.
-
Accurately apply both direct and indirect strategies.
-
Score at least 7/10 correct in the tutorial within 1 hour.
INDUCTION
Time to wake up that brain! This crossword is here to help you refresh your Cartesian Plane knowledge in a fun way.
MATERIAL
TUTORIAL
Set 1: Cartesian Coordinates & Distance Formula
Duration : 1 hour
Answer the Following Exercise
-
Plot the points (2, 3) and (5, 7) on the Cartesian plane.
-
Identify the quadrant for the point (−4, 6).
-
Find the distance between (1, 2) and (4, 6).
-
Calculate the midpoint between (−3, 5) and (3, −1).
-
A square has corners at (1,1) and (5,1). Find the length of one side.
-
Determine if triangle with points A(0,0), B(3,4), and C(3,0) is right-angled.
-
A circle has diameter endpoints at (−2, 4) and (6, 8). Find the centre and radius.
-
In a coordinate layout, two machines are located at A(2,3) and B(10,15). Calculate the exact distance and suggest shortest cable route.
-
A robotic arm moves from point A(2,5) to point B(10,9). Calculate the linear travel distance of the arm.
-
A CNC machine table has two drill positions at (0,0) and (6,8). What is the diagonal distance between the drills?
ACTIVITY 1
Collaborative Activity (Pair Work)
Durations : 20 Minutes
Title: Coordinate Geometry in Real Objects
Instructions:
-
In pairs, choose one technical object around you (e.g. a mechanical tool, electronic device, or classroom equipment).
-
Identify two distinct components within the object.
-
Trace the positions of these two components and represent their locations using coordinates on a Cartesian plane. You may assign your own coordinate system (e.g., origin at the bottom-left of the object).
-
Using the coordinates, calculate:
-
The distance between the two components.
-
The midpoint between them.
-
-
Record your findings and be prepared to share with the class.
- DOWNLOAD ACTIVITY SHEETS
ACTIVITY 2
📝 Project Task (Instructions):
Duration : 1 Hour
You are required to design an infographic OR a mind map to show real-world applications of the Distance and Midpoint formulas in various fields such as:
-
Engineering / Technical fields
-
Navigation / Mapping / GPS
-
Architecture / Construction
-
Robotics / Design
-
Sports analytics, etc.
💡 What to include in your infographic or mind map:
-
At least 2 real-world applications for each concept:
-
2 for Distance formula
-
2 for Midpoint formula
-
-
Brief explanation (1-2 sentences) of how each application works.
-
Visual elements (icons, diagrams, color-coding) to enhance clarity and engagement.
-
Must be organized, easy to read, and creatively presented (digital or hand-drawn).
✅ Rubric Pemarkahan (20 Marks Total)
| Criteria | Explanation | Marks |
|---|---|---|
| 🔍 Content Accuracy | Applications of distance and midpoint are correct and relevant. | 5 |
| 🎯 Clarity & Explanation | Explanations are clear and easy to understand. | 5 |
| 🎨 Visual Presentation | Design is attractive, good use of colors, icons and graphics. | 5 |
| 📚 Organization & Layout | Information is well organized and logically arranged. | 3 |
| ✨ Creativity & Effort | Shows creativity and effort in visual presentations. | 2 |
| Total | 20 |
🎯 Tips to Answer
-
You may use tools like Canva, Piktochart, MindMeister, or hand-drawn artwork.
-
Refer to your class notes and real-world examples for inspiration.
CONCLUSION
OVERVIEW
✅ Learning Outcomes Summary:
Students should be able to:
-
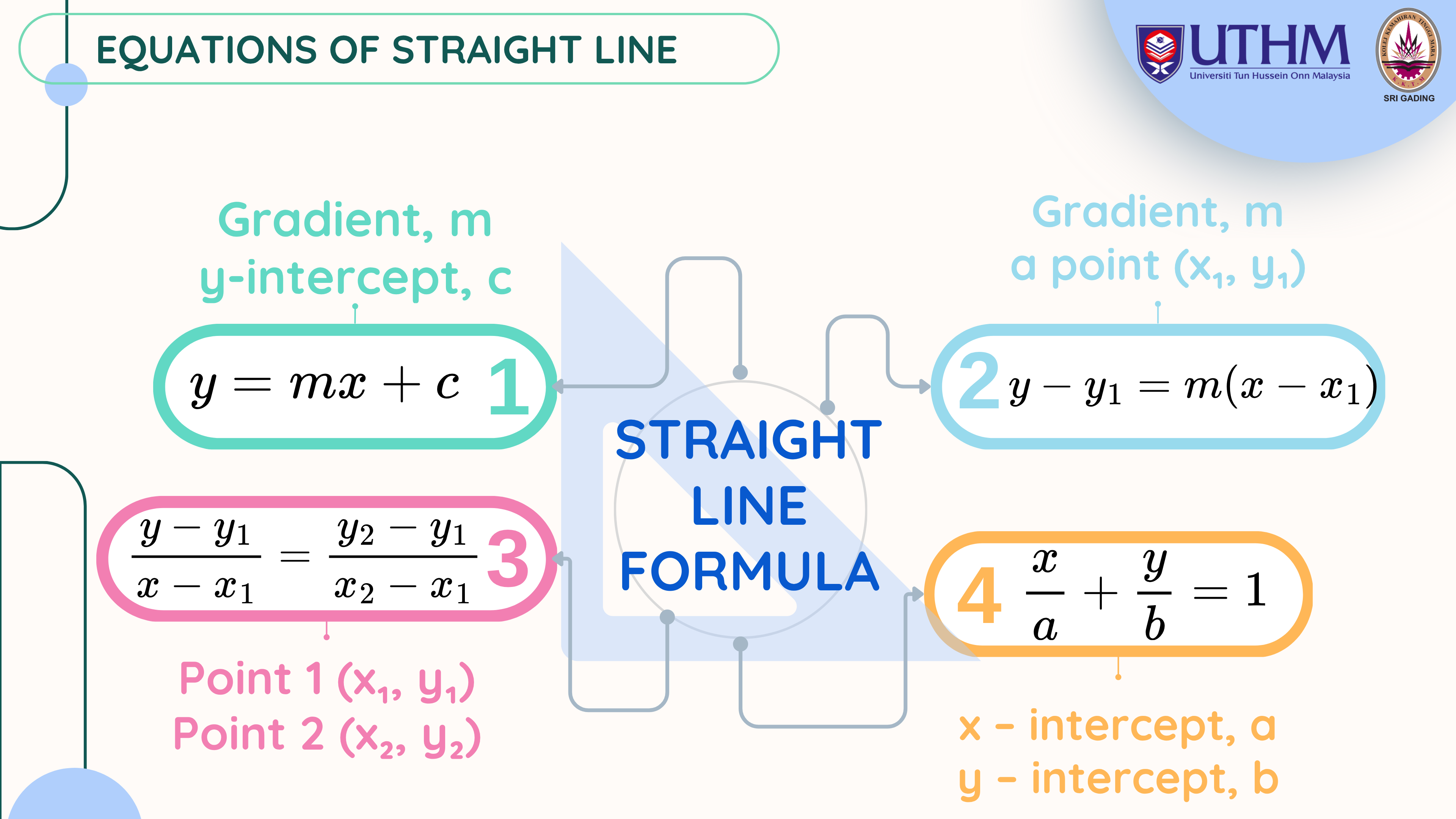
Identify and apply the correct straight line formula based on info given.
-
Form equations of straight lines using various methods.
-
Solve for unknowns in line equations.
-
Score 8/10 questions in 30 minutes.
INDUCTION
Read the following comic strips and identify the applications of equations in engineering.


MATERIAL
TUTORIAL
Set 2: Equations of Straight Line
Duration : 30 minutes
Answer the Following Exercise
-
Write the equation of a line with slope 2 and y-intercept 3.
-
Form the line equation passing through (0, 5) with slope −1.
-
Find the equation of the line passing through (1, 2) and (3, 6).
-
Convert the line (y = 2x + 3) into general form.
-
A line has x-intercept 4 and y-intercept −2. Write in intercept form.
-
Determine whether the point (4,11) lies on the line (y = 2x + 3).
-
A line passes through (2,−3) and is parallel to (y = 4x + 1). Find its equation.
-
Find the equation of a line perpendicular to (y = x − 4) and passing through (6,2).
-
In an automated conveyor design, the belt moves in a straight line from point (2,3) to (8,9). Find the equation of the belt’s path.
-
A part on an assembly line travels in a straight line and reaches the x-axis at x = 6 and y-axis at y = 4. Form the equation using intercept form.
ACTIVITY
Title: Exploring Straight Lines in the Real World
Duration: 1 Hour
Group: Pair work (2 students)
Instructions:
🧠 Task Description:
Work together in pairs to observe your surroundings (classroom, lab, campus, etc.) and identify an object or structure that contains or follows a straight line (e.g., edge of a whiteboard, window frame, floor tiles, railing, conveyor path, etc.).
Then:
-
-
Take a photo or draw the object and label at least two key points on the line.
-
Use an appropriate method (e.g., slope-intercept, two-point form, or intercept form) to determine the equation of the straight line.
-
Explain briefly which method you used and why.
-
Present your findings in a short report or visual presentation (digital or hand-drawn).
-
📊 Assessment Rubric (Total: 20 marks)
| Criteria | Explanation | Marks |
|---|---|---|
| 🔍 Identification of Object | Object chosen clearly contains a straight line relevant to the task. | 3 |
| 📍 Point Selection | Two appropriate points are selected and labeled clearly. | 3 |
| 🧮 Correct Equation | Equation of the straight line is calculated correctly using a suitable method. | 6 |
| 💬 Justification & Method | Clear explanation of the method used and the reasoning behind the choice. | 4 |
| 🎨 Presentation & Effort | Work is neat, organized, creative (photo, sketch, diagram), and shows teamwork. | 4 |
| Total | 20 |
CONCLUSION
OVERVIEW
✅ Learning Outcomes Summary:
Students should be able to:
-
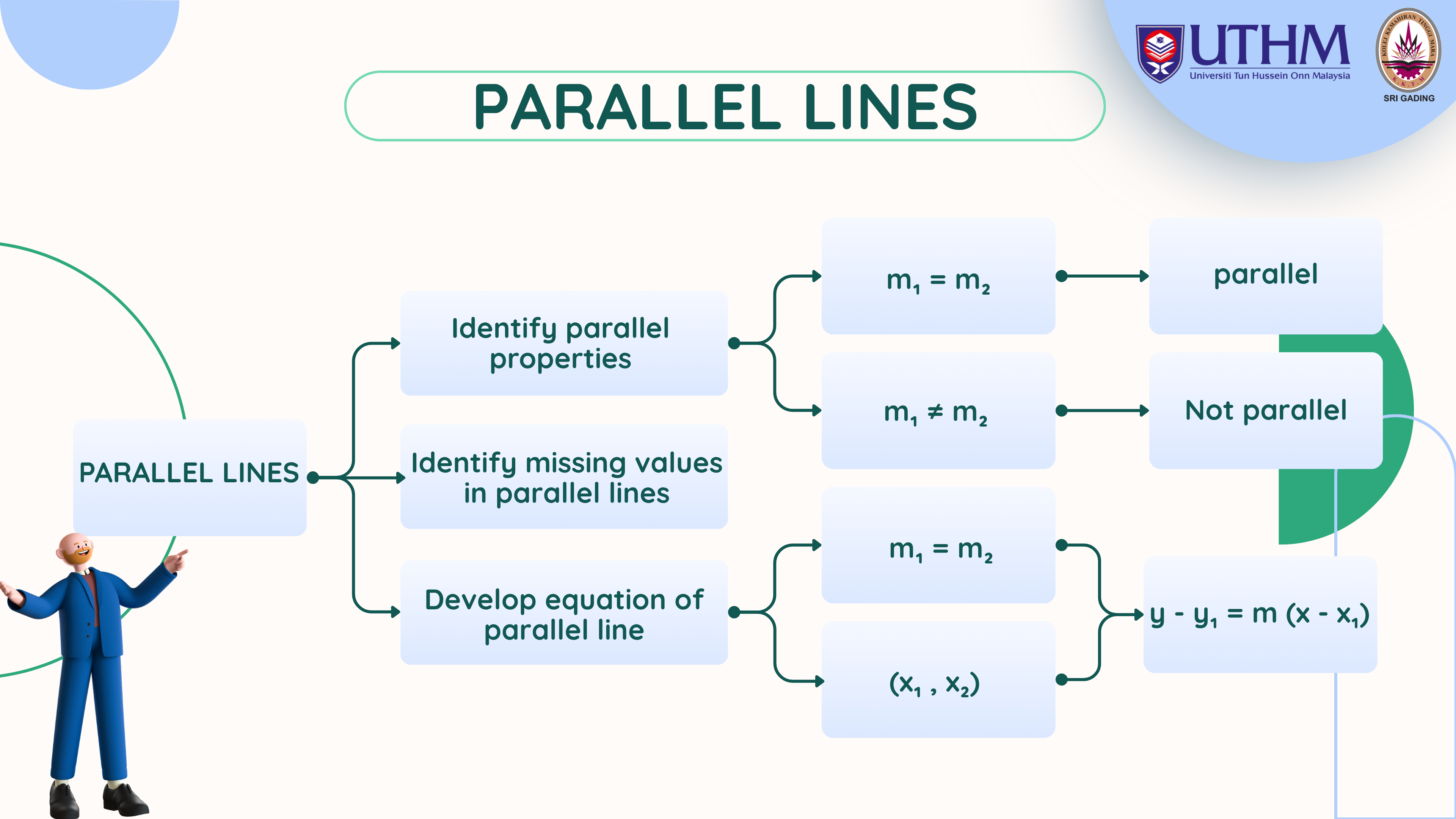
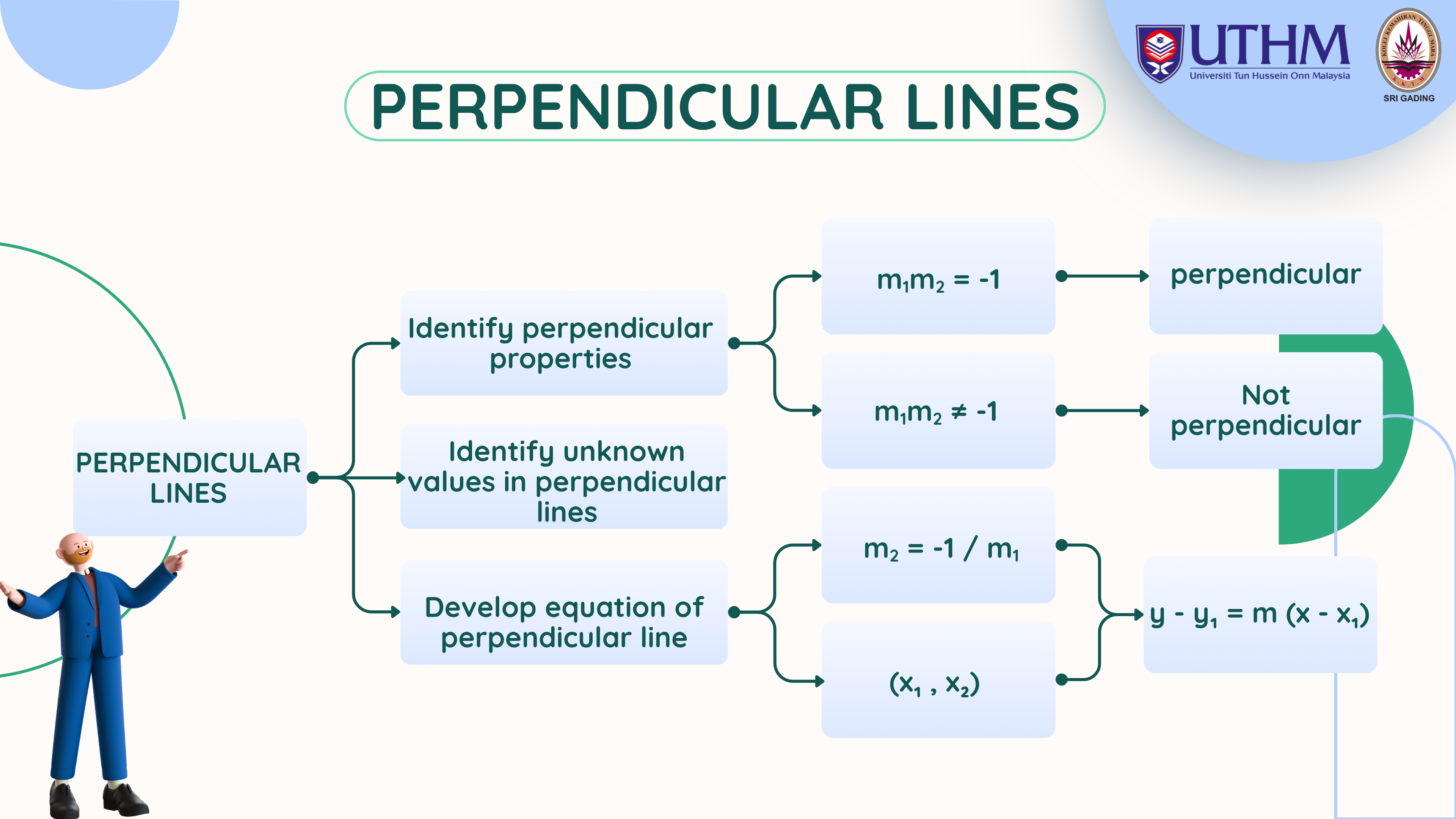
Determine if lines are parallel/perpendicular based on gradients.
-
Calculate unknowns using parallel or perpendicular properties.
-
Form equations of lines that are parallel or perpendicular to a given line.
-
Solve 8 out of 10 tutorial questions in 30 minutes.
INDUCTION
Rearrange the sentence to determine the properties of parallel and perpendicular lines.
MATERIAL
TUTORIAL
Set 3 : Parallel and Perpendicular Lines
Duration : 30 minutes
Answer the Following Exercise
-
Write the equation of a line with slope 2 and y-intercept 3.
-
Proof that the two lines y - 4x + 8 = 0 and 3y – 12x = 1 are parallel.
-
Find the gradient of line perpendicular to y = -8x + 3.
-
Determine if lines y = 2x + 5 and y = −0.5x − 3 are perpendicular.
-
Given a point (1,2), construct a line parallel to y = −3x + 7. That passing through this line.
-
Determine whether two points form a line perpendicular to (y = x).
-
Sketch two lines that are perpendicular and intersect at (0,0).
-
A design frame requires a beam to be perpendicular to a given reference line. Given the line (y = 2x − 4), construct the perpendicular beam passing through (3,1).
-
Two parts are aligned at angles given by (y = 5x + 2) and (y = −x + 7). Show if alignment is correct (i.e. perpendicular).
-
In a circuit board layout, two conductive paths must be parallel. One path follows the lane with equations of y = 0.75x + 5. Design another path through point (2,3).
ACTIVITY
🎬 Multimedia Task: Applications of Parallel and Perpendicular Lines
Duration: 1 Hour
Submission Format: Video or multimedia presentation
Tools Suggested: Any AI or digital content creation platform (e.g. Canva, Lumen5, Veed.io, CapCut, Adobe Express, etc.)
📝 Task Instructions:
You are required to work individually or in pairs to create a short video or multimedia presentation (1–3 minutes) that demonstrates real-world applications of parallel and perpendicular lines in your field of study (e.g. engineering, architecture, robotics, construction, automotive, etc.).
Your multimedia must include:
-
Definition and characteristics of parallel and perpendicular lines.
-
At least 1 real-world applications related to your diploma program for each lines.
-
Use of relevant images, icons, or videos.
-
A brief explanation (voiceover or text) describing how the applications involve parallel lines.
-
Creativity and clarity in delivery.
📊 Assessment Rubric (Total: 20 marks)
| Criteria | Explanation | Marks |
|---|---|---|
| 🧠 Content Accuracy | Concepts of parallel lines and applications are correct and relevant. | 5 |
| 🧩 Application Relevance | Chosen examples relate well to student's field of study or industry context. | 4 |
| 🔈 Explanation & Clarity | Information is clearly explained (via text or narration), easy to understand. | 4 |
| 🎨 Multimedia Design | Visually appealing with good use of icons, images, or video clips. | 4 |
| ✨ Creativity & Effort | Evident creativity, originality, and effort in the video or presentation. | 3 |
| Total | 20 |
💡 Tips for Students:
-
Keep your video short and focused (1–3 minutes).
-
Use templates if needed for a fast and professional result.
-
You may add subtitles or AI voiceovers if you're shy about recording your voice 😄.
-
Cite or credit sources/images if taken from the web.
CONCLUSION
OVERVIEW
✅ Learning Outcomes Summary:
Students should be able to:
-
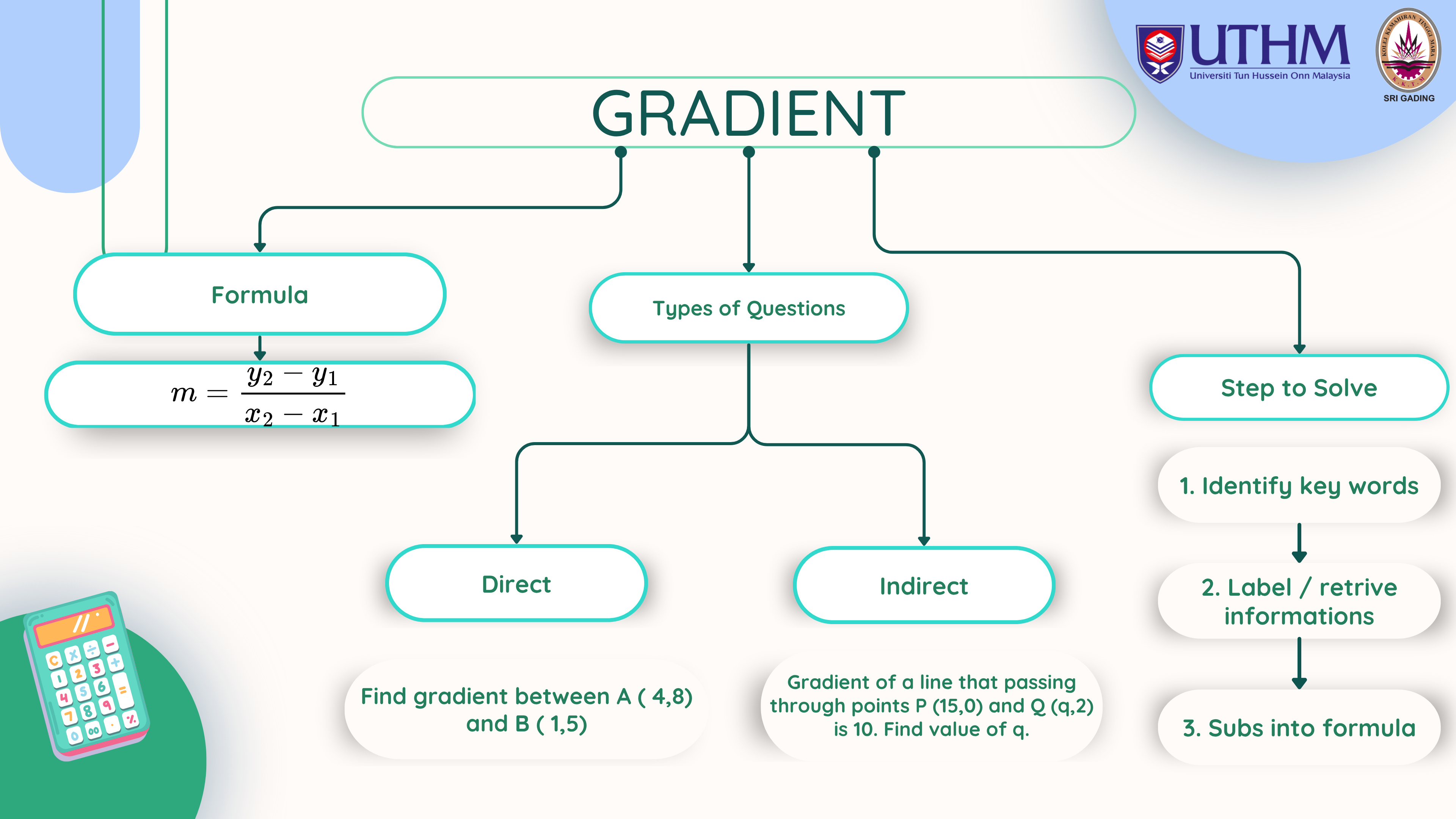
Calculate the gradient using two points.
-
Use gradient to determine line types (positive, negative, etc.).
-
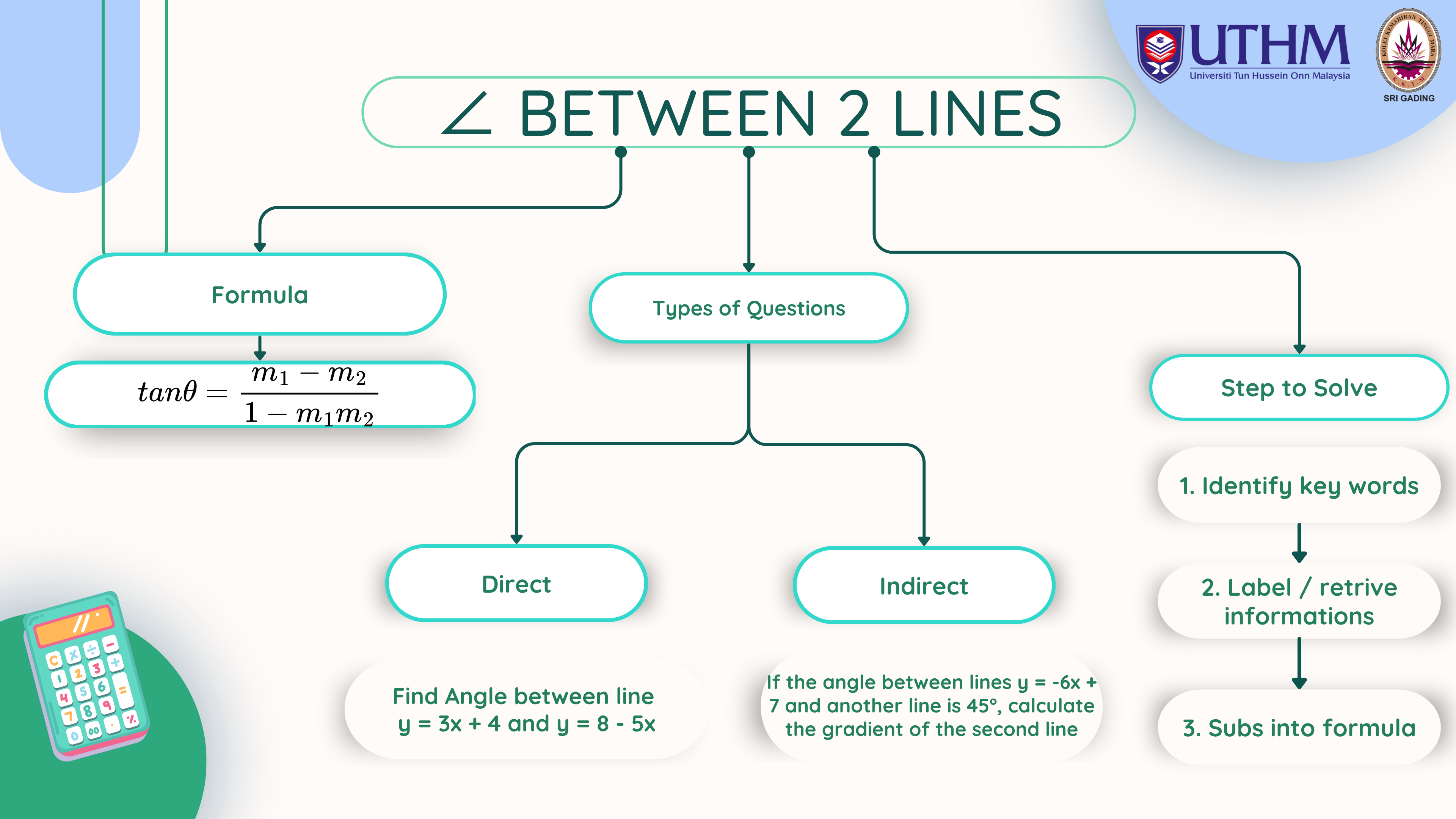
Apply angle formula between two lines.
-
Solve unknowns based on given angle.
-
Score at least 8/10 in tutorial questions within 30 minutes.
INDUCTION
🎯 Quick Task: Watch & Identify Angle in Engineering
⏰ Duration: 5 minutes
📺 Watch: This short video
📝 Instructions:
-
Watch the video once or twice.
-
Look for where angles are used in the machines or actions shown.
-
In 1–2 sentences, write how angle is applied in the video (e.g. cutting, lifting, rotating, etc.).
-
Submit your answer to your lecturer or on the platform provided.
MATERIAL
TUTORIAL
Set 4 : Gradient and Angles Between Lines
Duration : 30 minutes
Answer the Following Exercise.
-
Find the gradient of a line passing through (1, 2) and (4, 5).
-
What is the gradient of a horizontal line?
-
Calculate angle between (y = 2x) and (y = −x).
-
Given slopes 3 and −1/3, find angle between lines.
-
Find gradient and angle between lines joining (2,3) to (5,7) and (5,7) to (8,3).
-
Interpret whether angle between two lines is acute, right or obtuse.
-
Two connecting rods form angles between their centre lines. If their slopes are 1 and 3, find the exact angle of intersection.
-
A structure requires a diagonal cross-brace forming a specific angle. Find the angle between (y = 2x) and (y = −3x + 5).
-
In bridge design, two beams meet with gradients of 1 and −1. Calculate the angle between them.
-
An inclined conveyor belt forms an angle of 20° with the horizontal. What is the gradient of the belt?
ACTIVITY
📝 Assignment Task: Literature Review on Coordinate Geometry Application
⏳ Duration: 1 Hour
📄 Submission Format: Short report / typed document (1–2 pages)
🧠 Objective:
To explore real-world problems that involve gradient and angle in Coordinate Geometry, and understand how these concepts are applied in engineering or technical fields.
🔍 Task Instructions:
You are required to:
-
Identify a real-world engineering or technical problem that involves gradient (slope) and/or angle from any online journal article, magazine, blog, or academic source.
-
Summarize the application of Coordinate Geometry in solving that problem.
-
Focus on how gradient and angle are used in analysis, design, construction, navigation, automation, or any relevant field.
-
Your write-up should include:
-
A brief problem description (1 paragraph)
-
An explanation of how gradient or angle is applied
-
Your reflection or opinion on its usefulness
-
Source citation (link or title of article/journal)
-
💡 Examples of Application Fields:
-
Road / highway design (gradient of slopes)
-
Robotic arm angle control
-
Roof truss angle in construction
-
Solar panel tilt optimization
-
Drainage slope design
-
Coordinate tracking in autonomous vehicles
📊 Assessment Rubric (Total: 20 marks)
| Criteria | Explanation | Marks |
|---|---|---|
| 🔍 Problem Relevance | Real-world problem clearly stated and related to Coordinate Geometry | 4 |
| 🧠 Concept Accuracy | Correct and appropriate use of gradient/angle concepts | 5 |
| 📚 Literature Integration | Source is relevant, clearly cited, and integrated in the explanation. | 3 |
| ✍️ Explanation & Clarity | Explanation is clear, organized, and easy to follow. | 4 |
| 💭 Reflection & Insight | Shows understanding and critical thinking about the application | 2 |
| 🗂️ Presentation & Formatting | Neat, well-structured, within 1–2 pages | 2 |
| Total | 20 |
🎯 Tips for Students:
-
Search with keywords like "slope in construction", "application of gradient in engineering", or "angle in robotic design".
-
Use trusted sources: Google Scholar, Engineering.com, ResearchGate, Medium, or reputable blogs.
-
Keep your explanation short but meaningful — focus on how and why gradient/angle is used.
-
Include diagrams or images if it helps you explain better (optional).
CONCLUSION

Hi! I'm Lyssa Daud, a dedicated lecturer in Engineering Mathematics. My teaching philosophy focuses on making mathematics engaging and accessible through active learning and innovative 21ˢᵗ century education methods.
"Don’t just deliver information. Create transformation."
Acknowledgement
This project is a collaborative initiative between the Centre for Virtual Learning (CVL), UTHM and Kolej Kemahiran Tinggi MARA Sri Gading (KKTM SG), dedicated to enhancing flexible educational opportunities and advancing lifelong learning on a global scale.
I would like to express my heartfelt gratitude to Prof. Madya Ts. Dr. D’oria Islamiah Rosli, Mr. Azman Ali, Ts. Lelasari Ali, and Ms. Al Dinnul Firdausi Mohd Ibrahim for their invaluable guidance, encouragement, and support throughout this journey.
My sincere thanks also go to Mr. Hemmy Abd Jalal, Mr. Mohd Hidzam Othman, Ms. Noorhidayah Jaafar, Ms. Syaza Nazurah Khamsa, Mr. Muhammad Zulkifli Che Lah, Ms. Siti Hasnah Hud, Ms. Halijah Sa’don, Ms. Nur Syuhada Nor'din, Ms. Nurul Afiqah Roslan, and Mr. Hairul Anuar Ahmaddariri for their contributions, collaboration, and continuous encouragement.
Your support has truly made a difference, and I am deeply grateful.
A special thanks to Madihah binti Yahaya, my partner throughout the LSI journey — thank you for sticking with me through thick and thin. 🌟






