Skip to main content

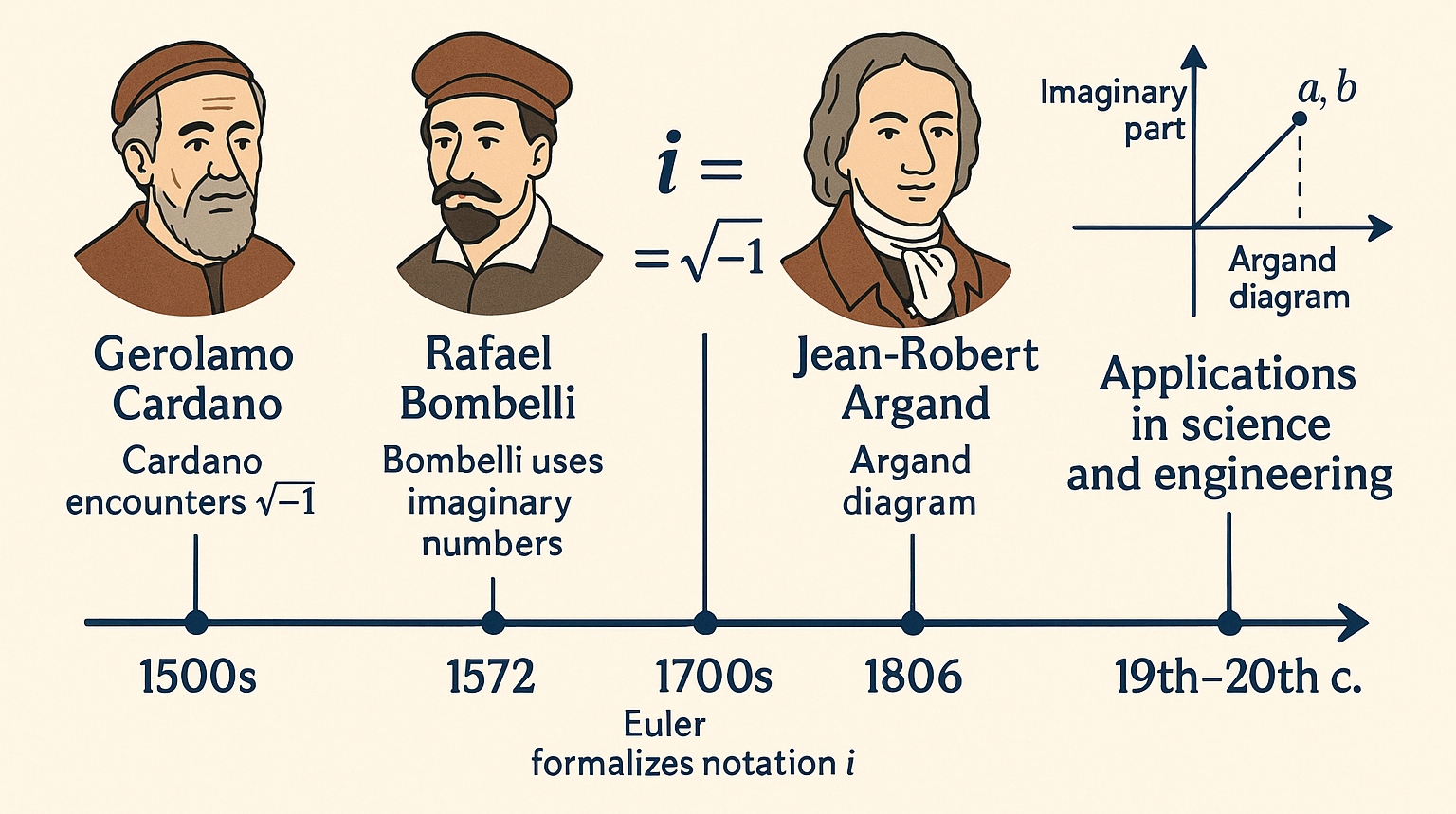
Complex numbers have an interesting story. In the 1500s, mathematicians like Cardano found them when trying to solve equations with the square root of negative numbers. At first, people thought they were strange and useless. In the 1600s, Bombelli started using them more seriously and made rules for them. Later, in the 1700s, Euler used the letter i to mean the square root of –1. In the 1800s, Gauss and Argand showed how to draw complex numbers on a plane, now called the Argand diagram. Today, complex numbers are very useful in science and engineering, especially in electricity and physics.

1.1 INTRODUCTION TO COMPLEX NUMBER

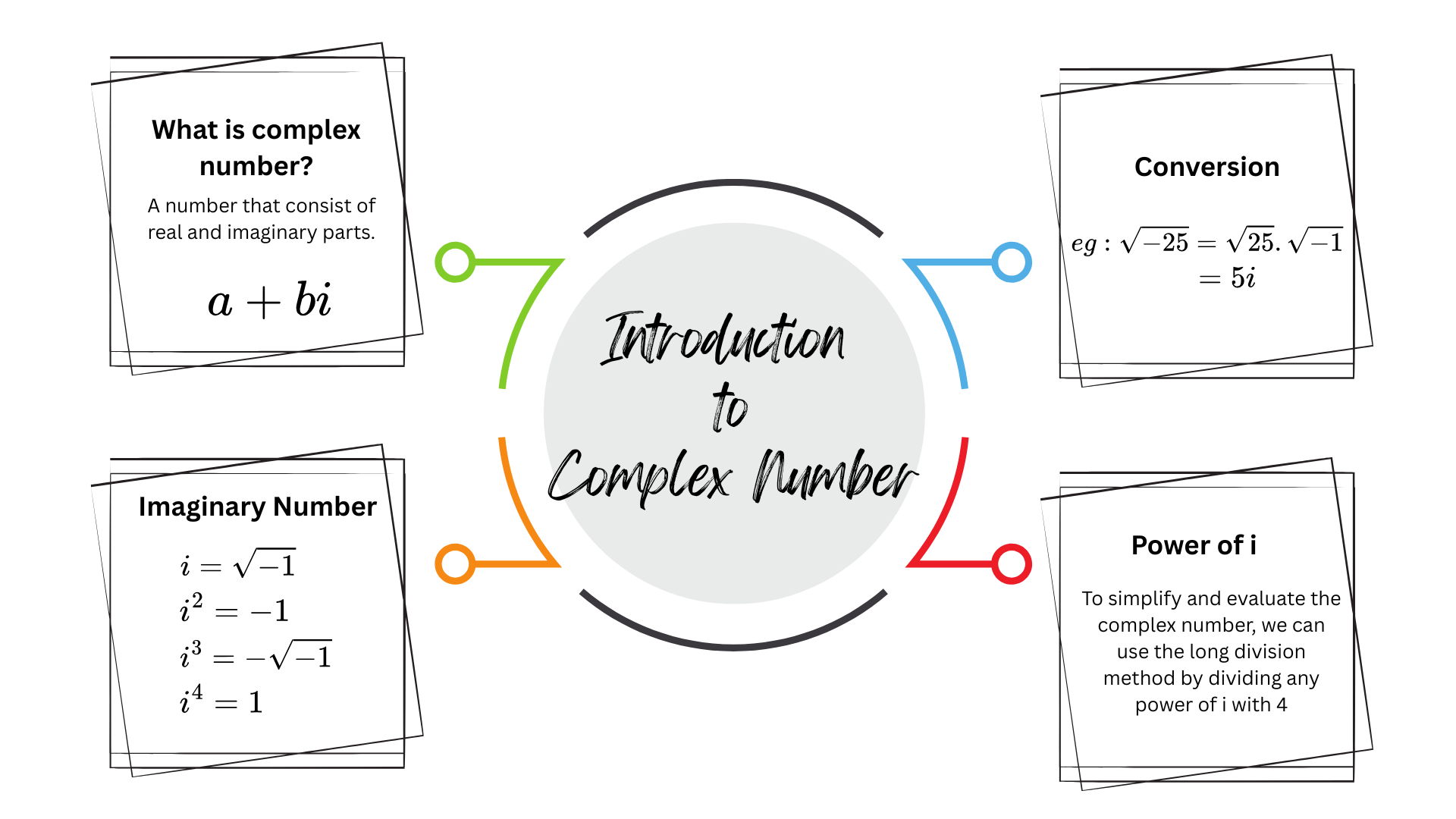
LO 1 : Write the square root of negative numbers in terms of i. Simplify and evaluate the powers of i.

1.2 COMPLEX NUMBER IN RECTANGULAR FORM AND ARGAND DIAGRAM

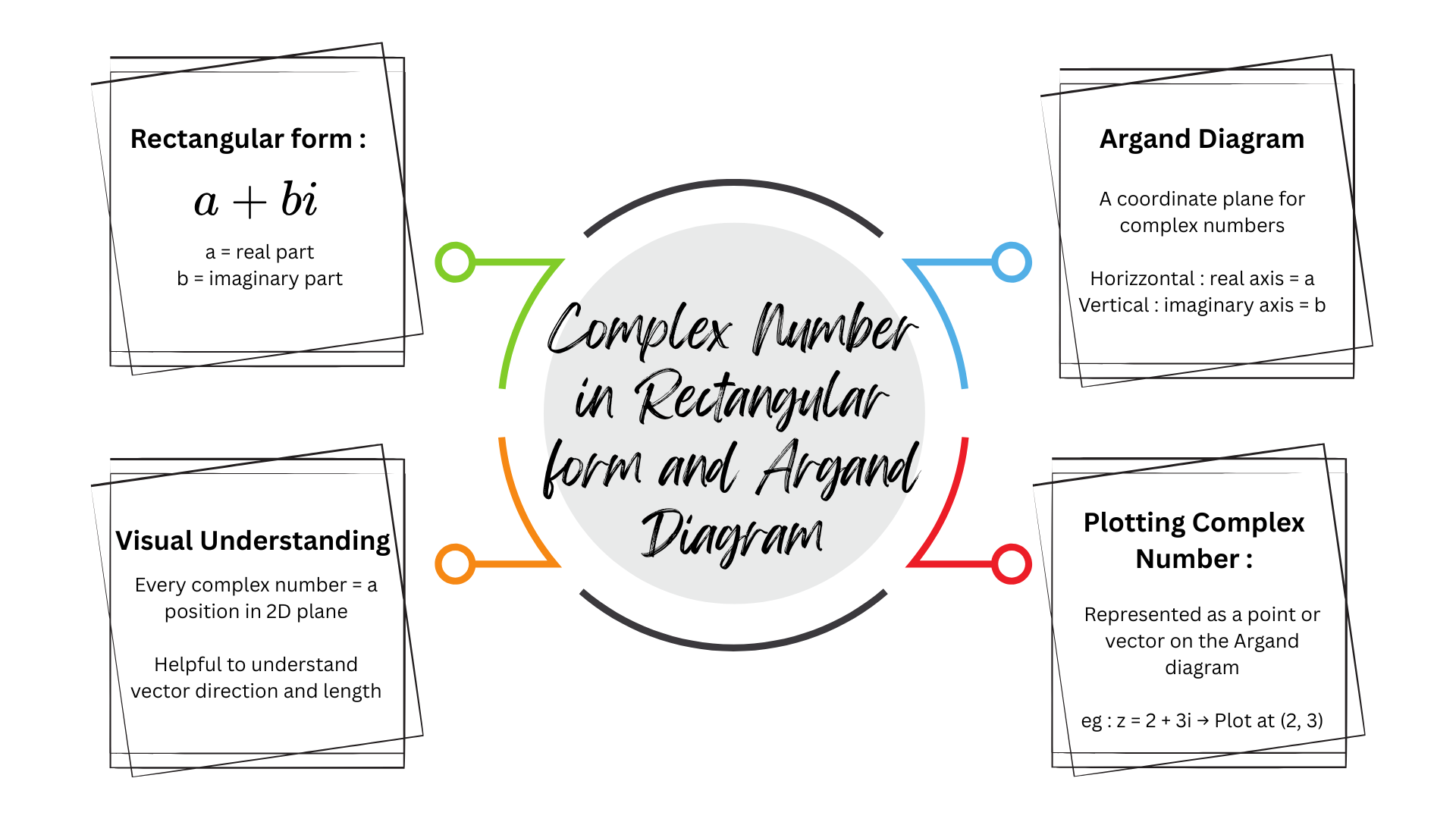
LO 2 : State complex number in rectangular form. Plot complex number in Argand Diagram.

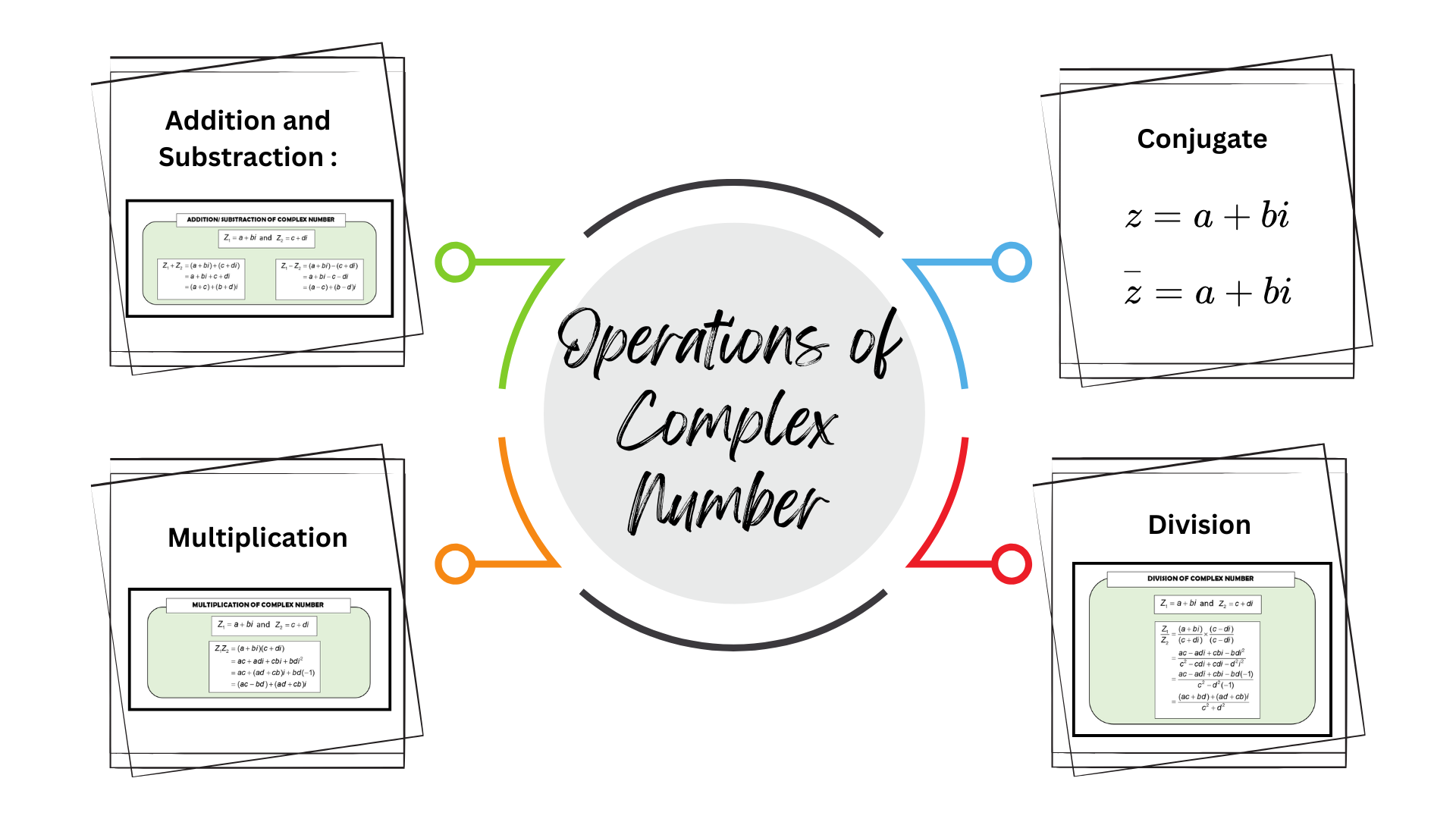
1.3 OPERATIONS OF COMPLEX NUMBER

LO 3 : Perform operations (addition, substraction, multiplication and division) of complex number. Perform division of complex numbers using the conjugate.

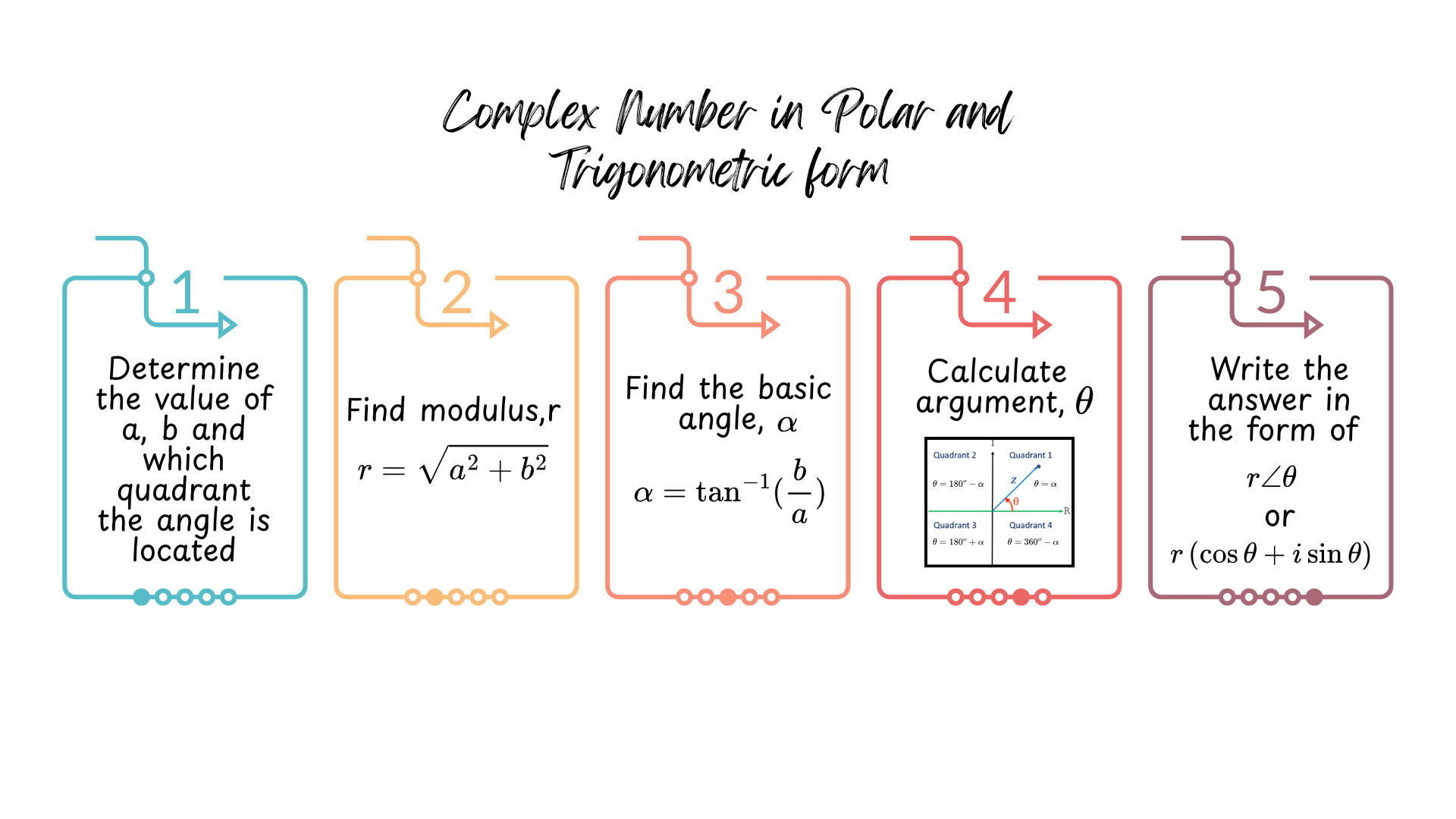
1.4 COMPLEX NUMBER IN POLAR AND TRIGONOMETRIC FORM

LO 4 : Calculate the modulus and argument of the complex number. Write complex number in polar and trigonometric form.

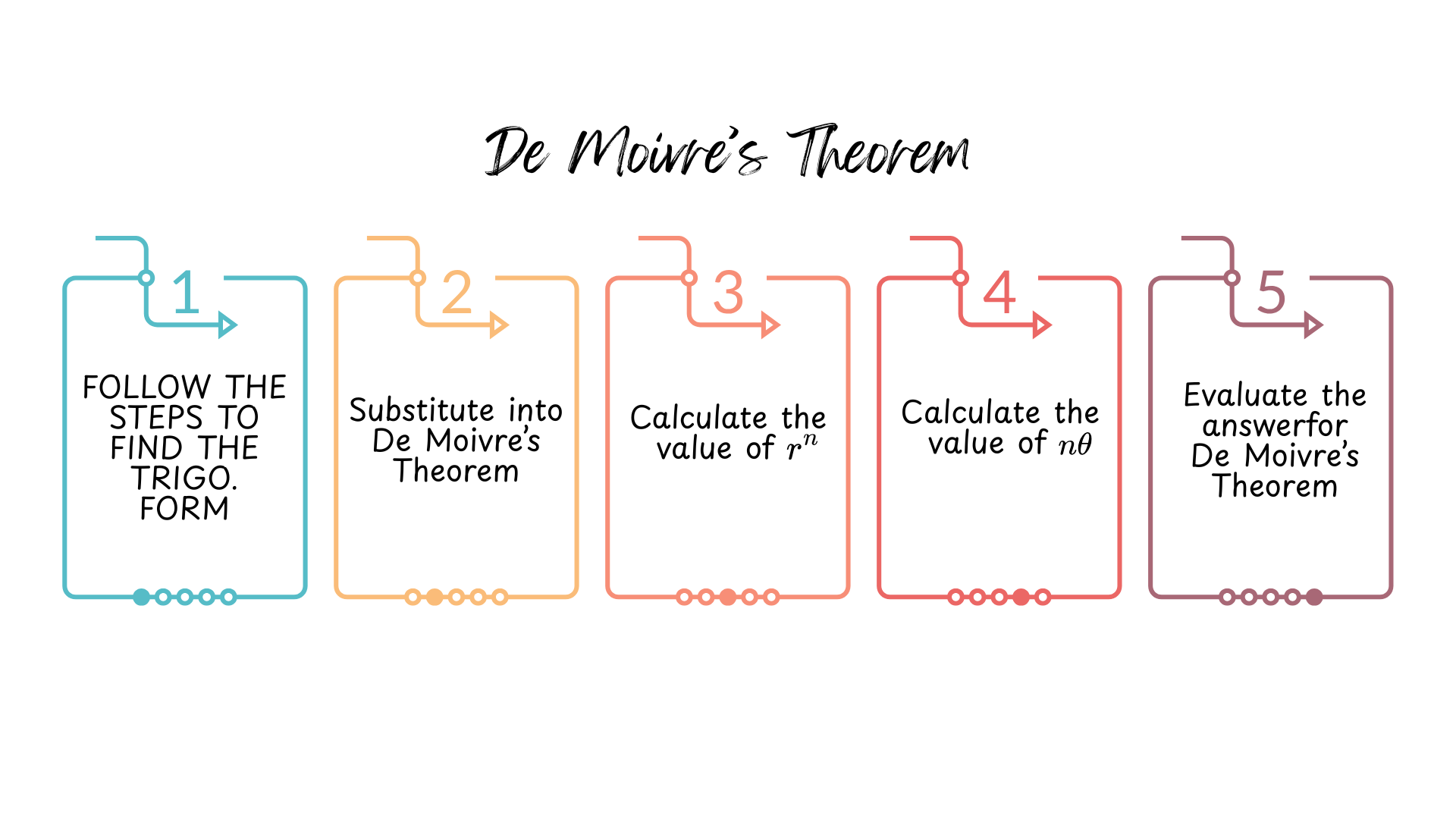
1.5 DE MOIVRE’S THEOREM

LO 5 : Use De Moivre’s Theorem to find powers of a complex number.

INDUCTION

LESSON MATERIAL

COLLABORATIVE ACTIVITY

TUTORIAL

PROJECT

📄 Job Sheet: Infographic / Mind Map Project

Subtopic: Introduction of Complex Number - Imaginary Number
Time Allocation: 1 hour

🎯 Task Objective

Create a mind map or infographic that clearly shows real-life applications of imaginary numbers in fields like science, engineering, or technology.

🔍 Project Instructions

  1. Choose your format:

    • Option A: Mind Map

    • Option B: Infographic

  2. Research real-life applications of imaginary. You may include areas such as:

    • Electrical engineering (AC circuits)

    • Quantum physics

    • Signal processing

    • Control systems

    • Computer graphics

    • Fluid dynamics

  3. Design your project using clear keywords, visuals, and structure:

    • Title

    • Short explanations (in your own words)

    • Diagrams / symbols / color coding

    • At least 3–5 real-life applications

  4. Tools: You need to create it digitally using tools like Canva, PowerPoint, Google Slides, or drawing software.

  5. Submit your final product and be ready to explain your work to the class.

CONCLUSION

INDUCTION

LESSON MATERIAL

COLLABORATIVE ACTIVITY

TUTORIAL

PROJECT

📄 Job Sheet: Drawing and Comparing Argand Diagrams

Subtopic: Argand Diagrams
Time Allocation: 1 hour

🎯 Project Objective

To plot complex numbers on an Argand diagram using graph paper and compare your plot with one created using interactive software like GeoGebra or any similar tool.

🧭 Project Instructions

  1. List at least 6 complex numbers (by yourself), including a variety of types:

    • Pure real (e.g., 3)

    • Pure imaginary (e.g., 4i)

    • Complex numbers with both real and imaginary parts (e.g., 2 + 3i)

  2. Plot the complex numbers on graph paper:

    • Label axes: real axis, a and imaginary axis, bi

    • Plot and label each complex number clearly

  3. Use interactive software (e.g., GeoGebra, Desmos, or any online Argand plotter):

    • Recreate the same Argand diagram

    • Ensure the points are clearly labeled

  4. Compare your manual and digital graphs:

    • Are all points in the same position?

    • Which method is easier/more accurate?

    • What did you learn from using both methods?

  5. Submit:

    • Your hand-drawn Argand diagram

    • A screenshot or printout of the digital version

    • A short reflection paragraph (3–5 sentences)

CONCLUSION

INDUCTION

LESSON MATERIAL

COLLABORATIVE ACTIVITY

TUTORIAL

PROJECT

📄 Job Sheet: Literature Review on Real-World Application of Complex Number

Subject: Complex Number
Time Allocation: 1 hour

🎯 Project Objective

To explore real-world problems that involve complex numbers and review an article or journal paper discussing its application in any field such as engineering, physics, computer science, or signal processing.

🧭 Project Instructions

  1. Identify a real-world problem where complex numbers are used. You may choose topics like:

    • Alternating Current (AC) in electrical engineering

    • Signal processing

    • Control systems

    • Quantum mechanics

    • Computer graphics

    • Fluid dynamics or vibration analysis

  2. Search and select one relevant article, journal paper, or academic source (can be from Google Scholar, ResearchGate, or other reliable sources). If you’re unsure, ask your teacher for help.

  3. Read the article and write a literature review (about 150–300 words) that includes:

    • Title of the article and author(s)

    • Summary of the real-world problem discussed

    • How complex numbers are applied in solving or analyzing the problem

    • Why the application is important or useful in that field

  4. Attach the article (printed or link), or include the reference in proper format (APA / MLA / simple citation).

  5. Submit your written review and references.

CONCLUSION

INDUCTION

LESSON MATERIAL

COLLABORATIVE ACTIVITY

TUTORIAL

PROJECT

📄 Job Sheet: AI Video / Multimedia Presentation – Polar & Trigonometric Form of Complex Numbers

Subtopic: Complex Numbers in Polar and Trigonometric Form
Time Allocation: 1 hour

🎯 Project Objective

To create an engaging and informative video or multimedia presentation using AI tools to explain the usage of polar or trigonometric form of complex numbers in real-world or mathematical contexts.

🧭 Project Instructions

  1. Choose your focus:

    • Explain how to convert a complex number to polar/trigonometric form

    • Show real-life or mathematical applications (e.g., in engineering, rotation, phasor diagrams, or AC circuits)

  2. Plan your content:
    Your video should include:

    • A brief explanation of the polar/trigonometric form

    • Step-by-step examples of conversion or usage

    • Real-life application or context (if possible)

    • Visual aids, such as Argand diagrams or animated elements

  3. Create your video using an AI tool of your choice:

    • Suggested tools: Canva Video, Lumen5, Veed.io, Animaker, Clipchamp, Powtoon

    • Use voice-over, background music, or text-to-speech (optional)

  4. Length: 1.5 to 3 minutes

  5. Submit:

    • Final video (link or file)

    • Brief write-up (3–5 sentences) on what you learned or enjoyed during the process

CONCLUSION

INDUCTION

LESSON MATERIAL

COLLABORATIVE ACTIVITY

TUTORIAL

PROJECT

📄 Job Sheet: Exploration Activity – Solving Powers of Complex Numbers

Subtopic: De Moivre’s Theorem
Time Allocation: 1 hour

🎯 Activity Objective

Explore and identify the most appropriate method for finding the power of a complex number, and explain why and how it works—especially focusing on De Moivre’s Theorem.

🧭 Activity Instructions

  1. Recall what you know:

    • Write the rectangular and polar/trigonometric forms of a complex number.

    • Example: z=2+2iz = 2 + 2i

  2. Investigate:

    • Try squaring and cubing the complex number using both:

      • Direct multiplication (rectangular form)

      • De Moivre’s Theorem:
        zn=rn(cos⁡(nθ)+isin⁡(nθ))z^n = r^n (\cos(n\theta) + i\sin(n\theta))

  3. Compare the results:

    • Do both methods give the same answer?

    • Which method is easier or more efficient?

  4. Present your findings:

    • A short write-up (150–200 words) or poster-style note that includes:

      • Steps used

      • Diagrams (optional: Argand representation)

      • Your conclusion: When is De Moivre’s Theorem most useful?

  5. Submit your write-up (typed or handwritten) with all working steps shown.

CONCLUSION

Hi! I’m Madihah Yahaya, a diploma-level lecturer in Engineering Mathematics. My mission is to make math more than just numbers and formulas—it's about curiosity, creativity, and real-world connection. I’m passionate about using active learning and modern teaching techniques to spark interest and help students truly enjoy learning math.

This project is a collaborative effort between Centre for Virtual Learning (CVL), UTHM and Kolej Kemahiran Tinggi MARA Sri Gading (KKTM SG), aimed at enhancing flexible educational opportunities and supporting lifelong learning globally.

Contributors:
Prof. Madya Ts. Dr. D'oria Islamiah Rosli,  Mr. Azman Ali, Ts. Lelasari Ali, Mr. Hemmy Abd Jalal, Mr. Mohd Hidzam Othman, Ms. Noorhidayah Jaafar, Ms. Syaza Nazurah Khamsa, Mr. Muhammad Zulkifli Che Lah, Ms. Siti Hasnah Hud, Ms. Halijah Sa'don, Mr. Mohd Esaruddin Ebas and Ms. Lyssa Daud
Thank you for your exceptional guidance, technical support and expertise and insightful feedback throughout this internship.